RSA

Terminiología

RSA
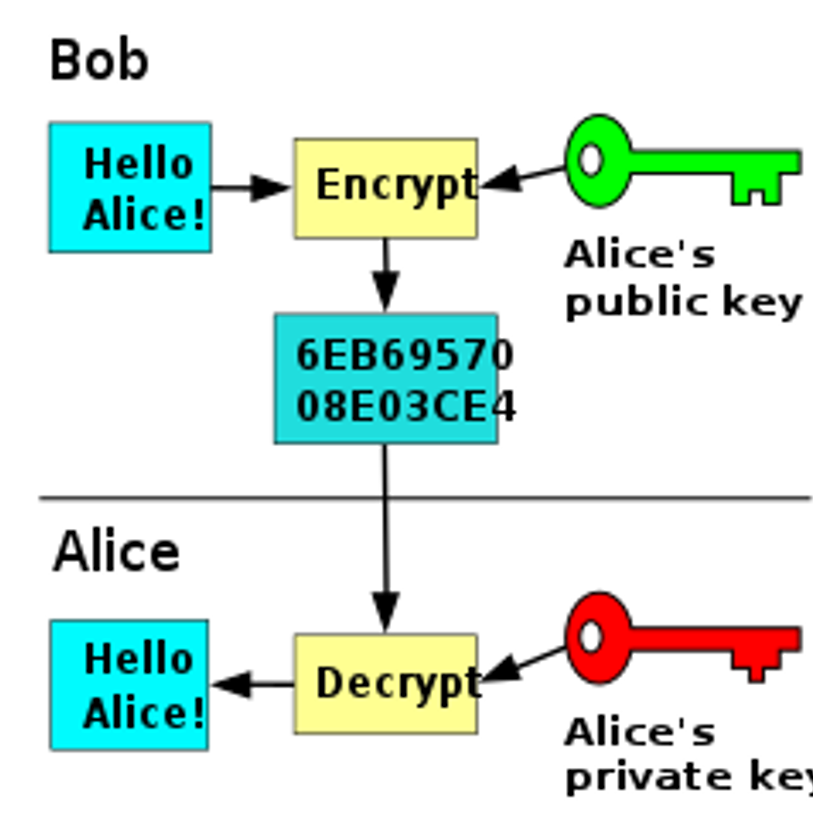
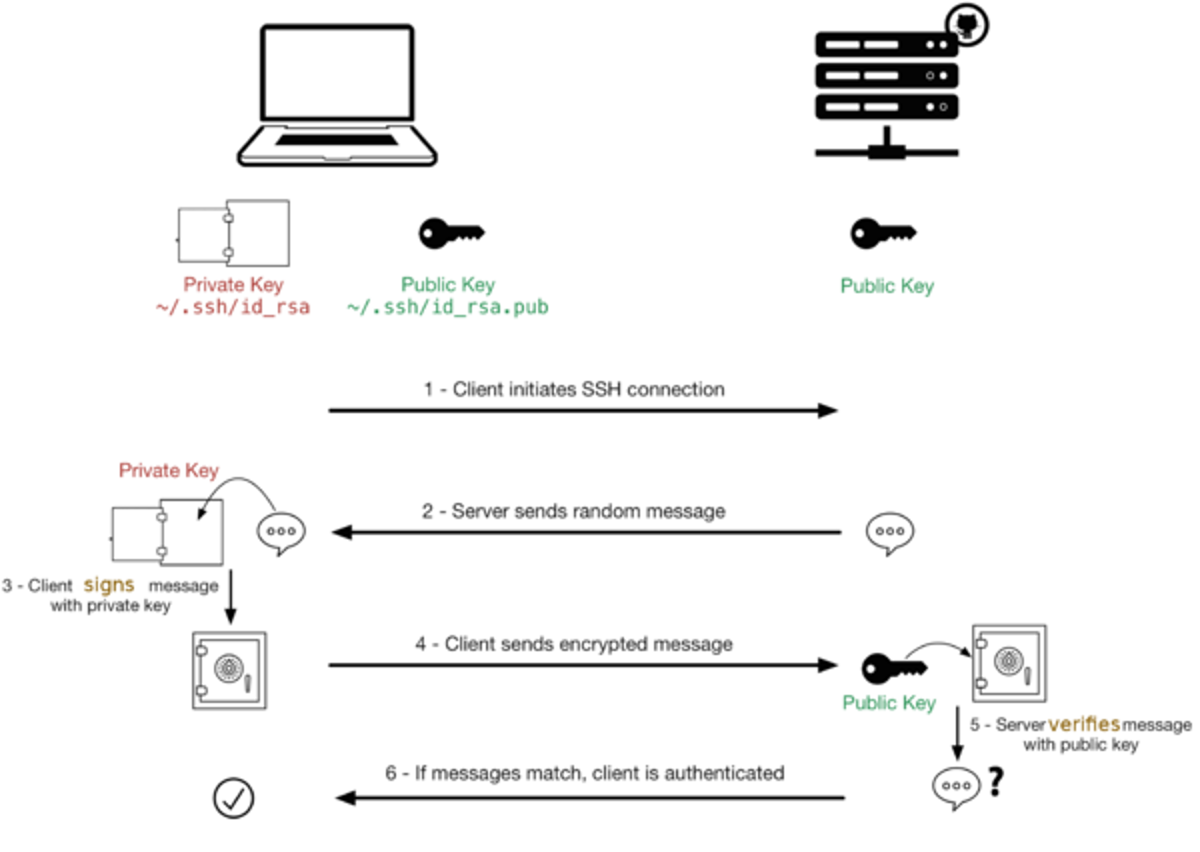
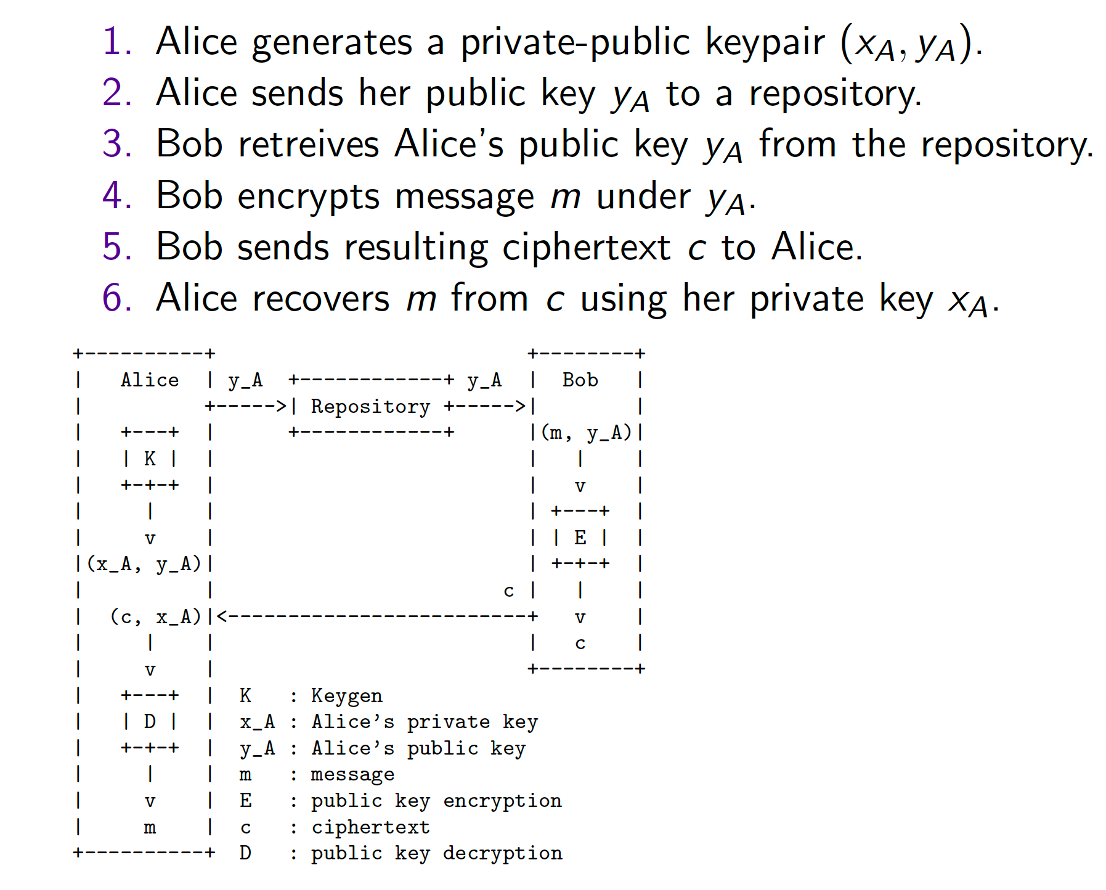
Public Key Encryption
  • Alice publica una llave publica derivada de una llave privada.
  • Todos pueden encriptar un mensaje para Alice usando la llave pública
  • Solo Alice puede descifrar el mensaje usando la llave privada.
RSA
Key Agreement

Los involucrados intercambian llaves publicas en un canal inseguro para establecer una llave secreta.

RSA
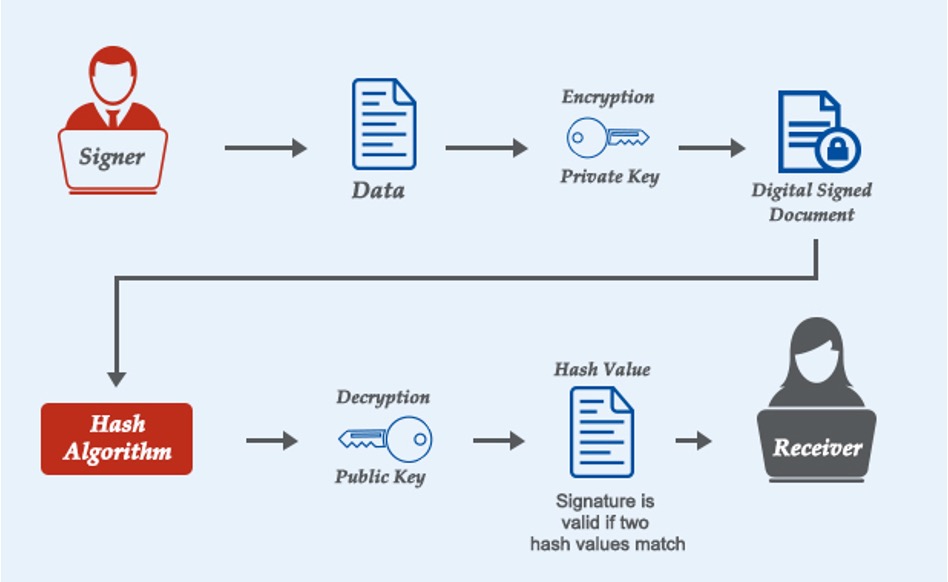
Digital Signature
  • Alice publica la llave publica derivada de la llave privada.
  • Alice firma el mensaje usando la llave privada
  • Cualquier persona puede validar el mensaje usando la llave publica
RSA

Definición

¿Qué es RSA?

  • Algoritmo de cifrado asimétrico
  • Basado en la factorización de números primos
  • Inventado en 1977 por Rivest, Shamir y Adleman
  • Utiliza el concepto de claves distintas para cifrado y descifrado.
  • Utilizado para cifrar y descifrar datos, autenticar la identidad digital y asegurar la comunicación en línea.

Aplicación

RSA se utiliza en una amplia variedad de aplicaciones como:
la encriptación de datos, la firma digital y la autenticación de usuarios.
Es uno de los algoritmos de cifrado más populares y ampliamente utilizados en la actualidad.

Principios Matemáticos

Factorización de Números Primos

RSA se basa en la dificultad computacional de factorizar grandes números en primos.

Dado un número grande que es el producto de dos números primos, encontrar esos factores (descomposición en primos) es computacionalmente costoso.

Generación de claves

El propietario de la clave privada selecciona dos números primos grandes, los multiplica para obtener un número llamado módulo, y usa este módulo para generar las claves pública y privada

Cifrado y Descifrado

El cifrado y el descifrado en RSA utilizan exponentes y operaciones modulares, aprovechando propiedades matemáticas que son fáciles de realizar, pero difíciles de invertir sin conocer los factores primos.

Claves Públicas y Privadas

RSA solo puede cifrar datos del tamaño del módulo (ej. 2048 bits ≈ 256 bytes). Si el mensaje es más corto, se rellena con padding. Los esquemas de padding agregan bytes de relleno siguiendo reglas específicas

Fórmulas

RSA

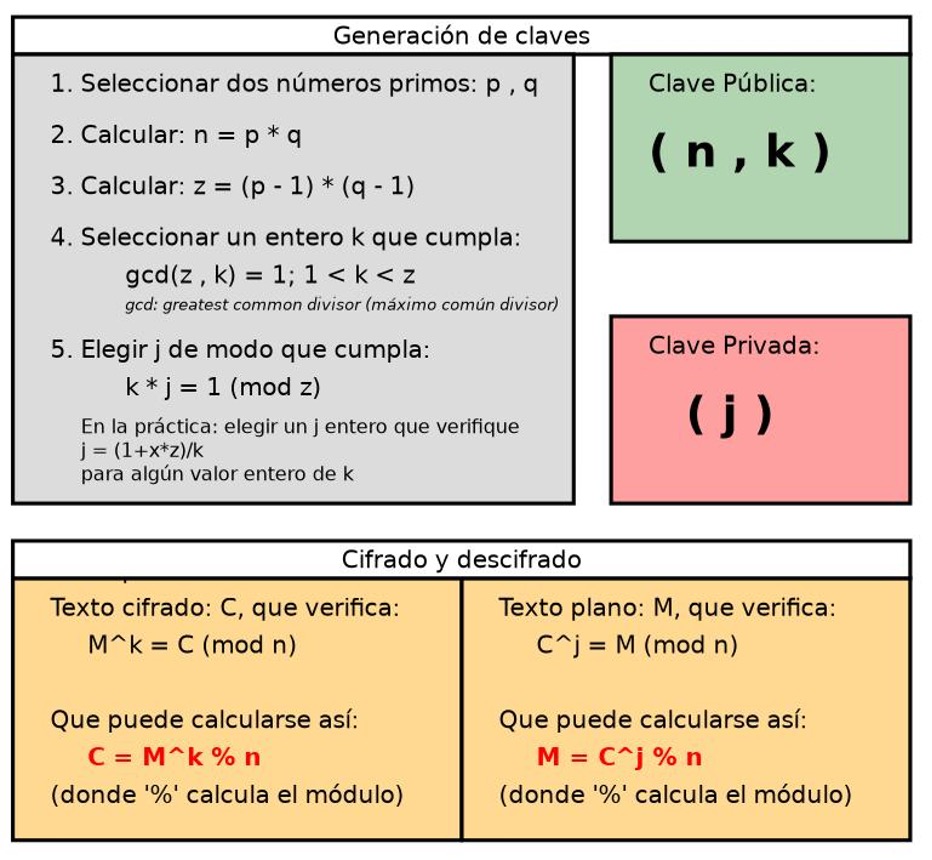
Generación de llaves

  • Supongamos que hemos elegido los números primos p = 61 y q = 53
  • Calculamos el módulo n = p * q
  • 61 * 53 = 3233
  • Calculamos la función de Euler z = (p-1)*(q-1)
  • 60 * 52 = 3120
  • Elección del Exponente de Cifrado k (Máximo común divisor)
  • Elegimos un exponente de cifrado k que sea coprimo con 3120
  • Supongamos que hemos elegido k = 17 ya que gcd(17, 3120) = 1

Generación de llaves

  • Elección del Exponente de Cifrado j (Máximo común divisor)
  • Calculamos j como el inverso multiplicativo modular de k módulo 3120.
  • En este caso, j = 2753
  • Ya que 17 * 2753 ≡ 1 (mod 3120).
  • Generamos las Claves
  • Clave pública es (n, e) = (3233, 17).
  • Clave privada es (n, d) = (2753).

Implementación

Encriptar

RSA

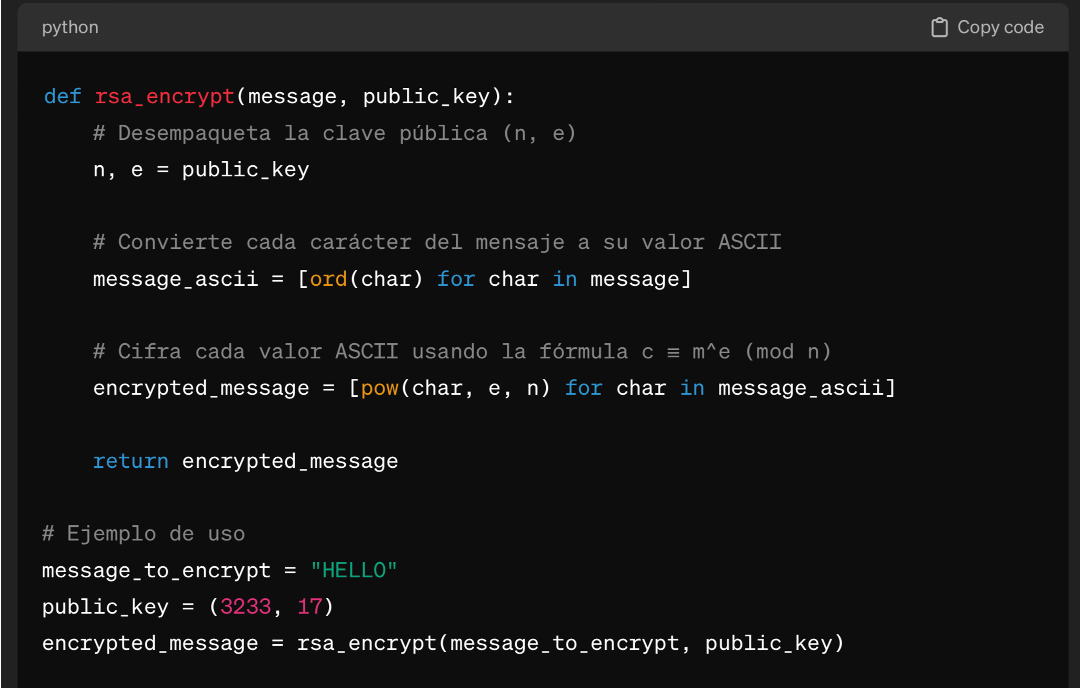
Encriptar

RSA

DesEncriptar

RSA

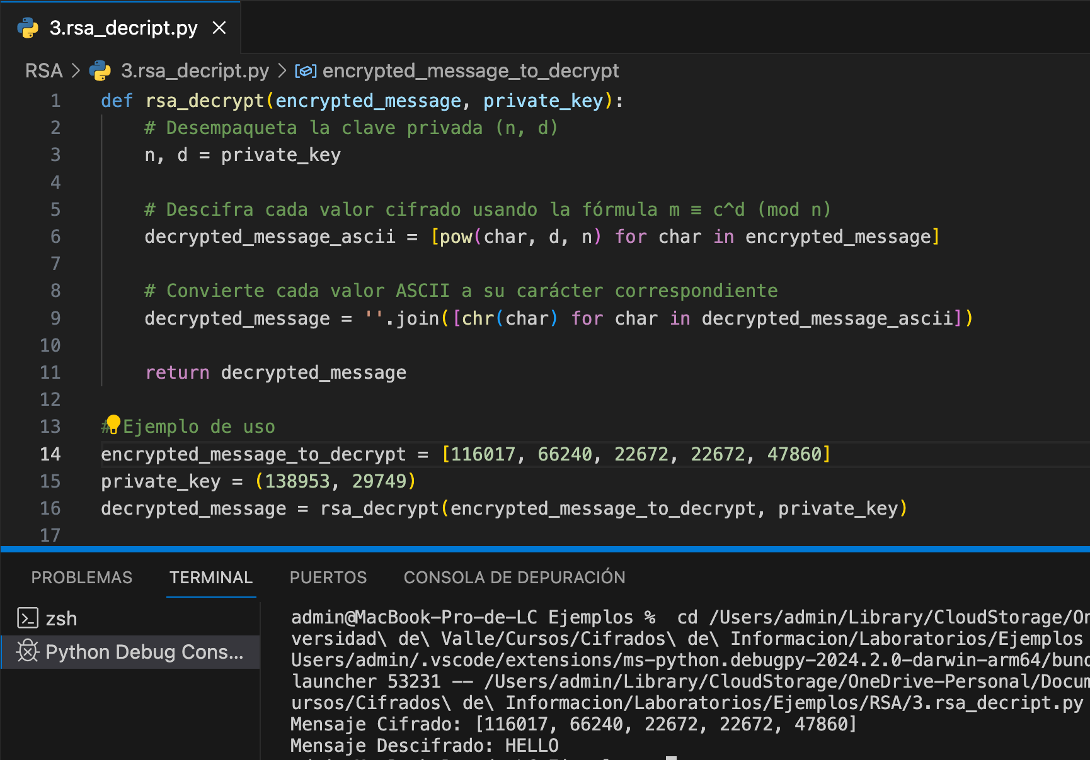
Implementación Python


                from Crypto.PublicKey import RSA
                key = RSA.generate(2048)
                private_key = key.export_key()
                public_key = key.publickey().export_key()
                print("Clave privada:", private_key.decode())
                print("Clave pública:", public_key.decode())

Seguridad y Aplicaciones

Seguridad

  • La seguridad de RSA se basa en la dificultad de factorizar números primos grandes.
  • La seguridad de RSA depende de la longitud de la clave.
  • Claves más largas son más seguras, pero también más lentas.
  • Claves de 2048 bits son comunes en la actualidad.

Firmas Digitales

  • Las firmas digitales son una forma de autenticación y verificación de la integridad de los datos.
  • Las firmas digitales en RSA se generan a partir de un mensaje y una clave privada.
  • El receptor puede verificar la firma usando la clave pública del emisor.

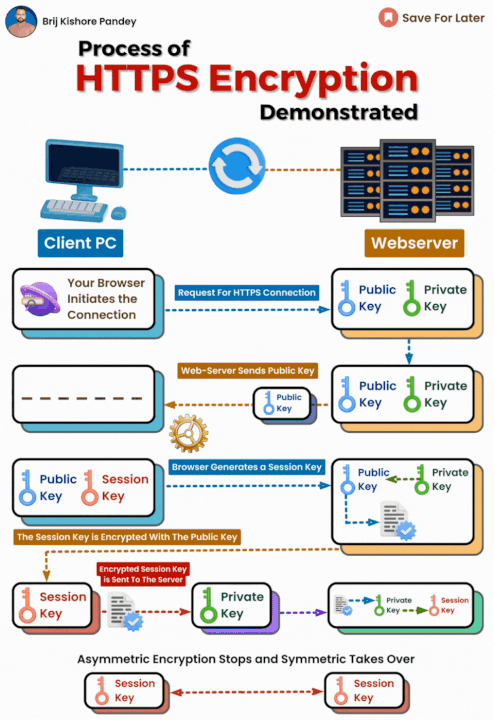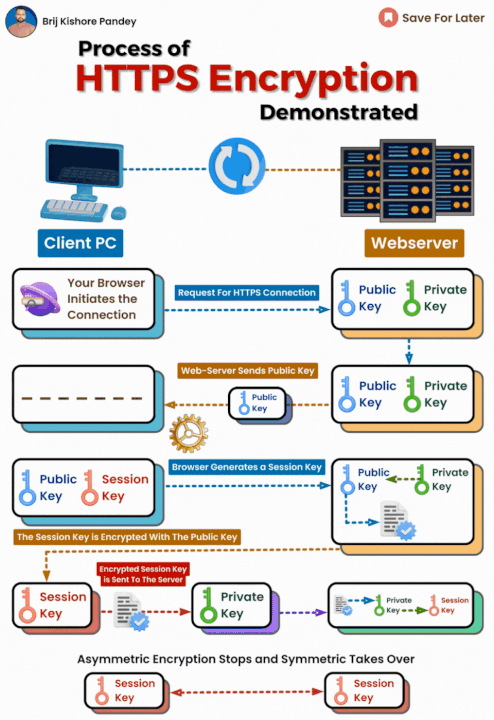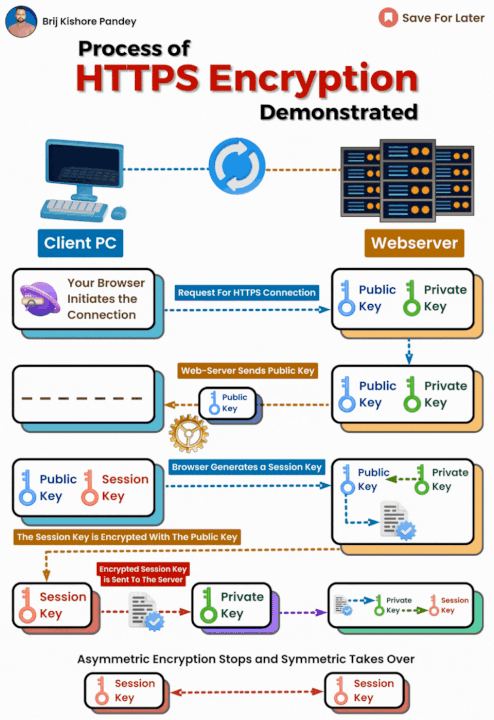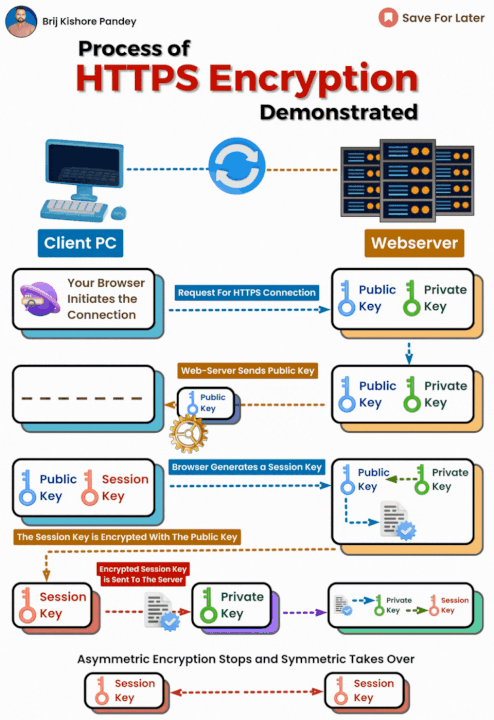
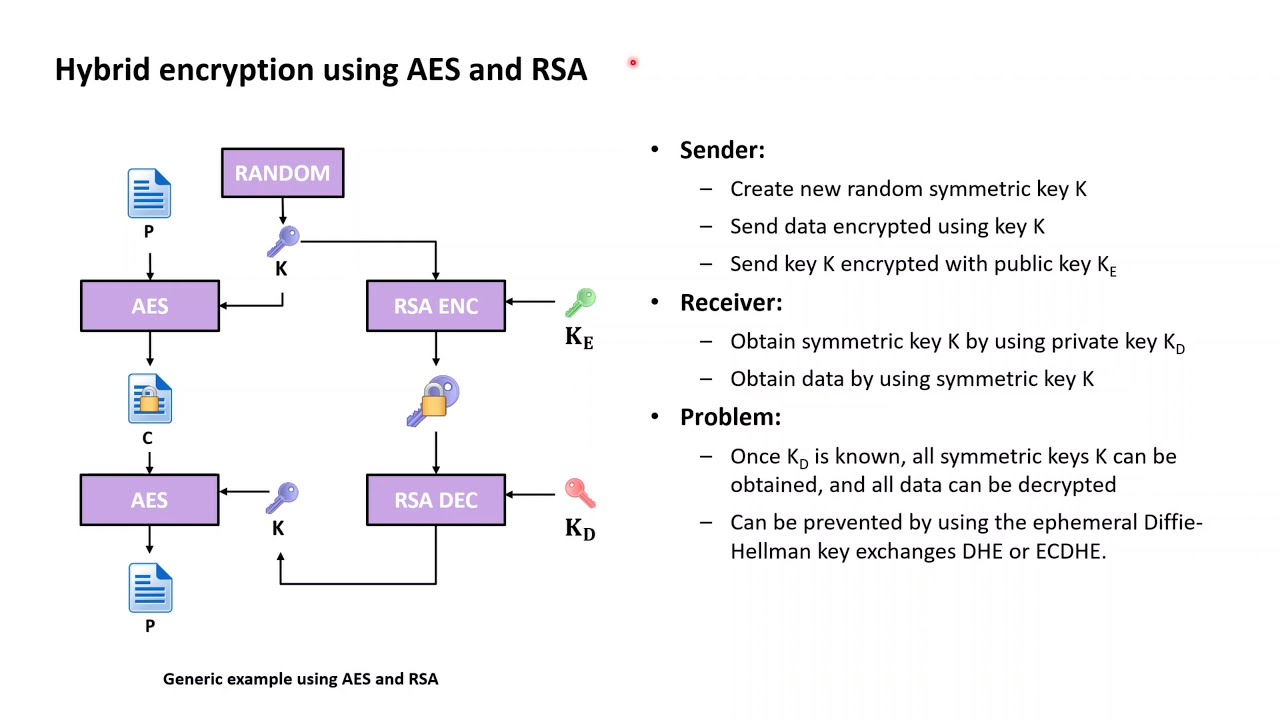
Cifrado de Clave Simétrica

RSA se utiliza a menudo para cifrar la clave simétrica utilizada en sistemas de cifrado simétrico, proporcionando así una capa adicional de seguridad.

Intercambio de Claves

RSA también se utiliza en el intercambio de claves de manera segura, permitiendo que dos partes acuerden una clave compartida sin revelar sus claves privadas.

Longitud de la Clave

La seguridad de RSA depende en gran medida de la longitud de la clave. Longitudes comunes de clave son 2048 bits y 3072 bits, pero se están considerando longitudes mayores para hacer frente a avances en capacidad computacional

Eficiencia

Aunque RSA es seguro, puede ser computacionalmente intensivo, especialmente con claves largas. Por esta razón, a menudo se utiliza en combinación con otros algoritmos para operaciones específica

Casos de Uso

  • TLS/SSL
  • Blockchain y Firmas Digitales
  • Combinación con AES
RSA
RSA
RSA
RSA